Walks Paths And Circuits

WALKS, PATHS AND CIRCUITS

Walk: A walk is defined as a finite alternative sequence of vertices and edges, of the form v_ie_j, v_i 1 e_j 1, v_i 2, ......., ekvm which begins and ends with vertices, such that
(i) each edge in the sequence is incident on the vertices preceding and following it in the sequence.
(ii) no edge appears more than once in the sequence, such a sequence is called a walk or a trial in G.

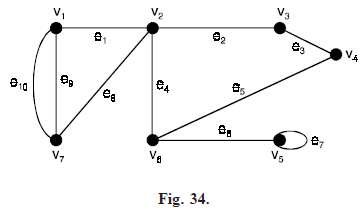
For example, in the graph shown in Figure 34, the sequences v₂e₄v₆e₅v₄e₃v₃ and v₁e₈v₂e₄v₆e₆v₅e₇v₅ are walks.

Note that in the first of these, each vertex and each edge appears only once whereas in the second each edge appears only once but the vertex v5 appears twice.
These walks may be denoted simply as v₂v₆v₄v₃ and v₇v₂v₆v₅v₅ respectively.

The vertex with which a walk begins is called the initial vertex and the vertex with which a walk ends is called the final vertex of the walk. The initial vertex and the final vertex are together called terminal vertices. Non-terminal vertices of a walk are called its internal vertices.

A walk having u as the initial vertex and v as the final vertex is called a walk from u to v or briefly a u – v walk.
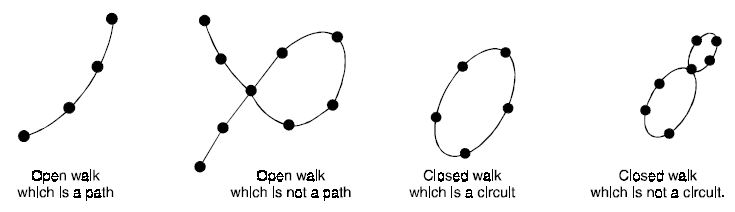
A walk that begins and ends at the same vertex is called a closed walk. In other words, a closed walk is a walk in which the terminal vertices are coincident.
A walk that is not closed is called an open walk.

In other words, an open walk is a walk that begins and ends at two different vertices.

For example, in the graph shown in Figure 34.

v₁e₉v₇e₈v₂e₁v₁ is a closed walk and v₅e₇v₅e₆v₆e₅v₄ is an open walk.

Path: In a walk, a vertex can appear more than once. An open walk in which no vertex appears more than once is called a simple path or a path. For example, in the graph shown in Figure 34.

v₆e₅v₄e₃v₃e₂v₂ is a path whereas v₅e₇v₅e₆v6 is an open walk but not a path.

Circuit: A closed walk with atleast one edge in which no vertex except the terminal vertices appears more than once is called a circuit or a cycle. For example, in the graph shown in Figure 34, v₁e₁v₂e₈v₇e₉v₁ and v₂e₄v₆e₅v₄e₃v₃e₂v₂ are circuits. But v₁e₉v₇e₈v₂e₄v₆e₅v₄e₃v₃e₂v₂e₁v₁ is a closed walk but not a circuit.

Note :

(i) In walks, path and circuit, no edge can appears more than once.
(ii) A vertex can appear more than once in a walk but not in a path.
(iii) A path is an open walk, but an open walk need not be a path.
(iv) A circuit is a closed walk, but a closed walk need not be a circuit.

Length: The number of edges in a walk is called its length. Since paths and circuits are walks, it follows that the length of a path is the number of edges in the path and the length of a circuit is the number of edges in the circuit. A circuit or cycle of length k, (with k edges) is called a k-circuit or a k-cycle. A k-circuit is called odd or even according as k is odd or even. A 3-cycle is called a triangle.

For example, in the graph shown in Figure 34,

The length of the open walk v6e6v5e7v5 is 2
The length of the closed walk v1e9v7e8v2e1v1 is 3
The length of the circuit v2e4v6e5v4e3v3e2v2 is 4
The length of the path v6e5v4e3v3e2v2e1v1 is 4
The circuit v1e1v2e8v7e10v1 is a triangle.

Note :

(i) A self-loop is a 1-cycle.
(ii) A pair of parallel edges form a cycle of length 2.
(iii) The edges in a 2-cycle are parallel edges.