Fluery's Algorithm

FLEURY’S ALGORITHM: Let G = (V, E) be a connected graph with each vertex of even degree.

Step 1. Select an edge e1 that is not a bridge in G.
Let its vertices be v1, v2.
Let π be specified by Vπ : v1, v2 and Eπ : e1.
Remove e1 from E and v1 and v2 from V to create G1.

Step 2. Suppose that Vπ : v1, v2, ...... vk and Eπ : e1, e2, .......ek – 1 have been constructed so far, and that all of these edges and vertices have been removed from v and E to form Gk – 1. Since vk has even degree, and ek – 1 ends there, there must be an edge ek in Gk – 1 that also has vk as a vertex.
If there is more than one such edge, select one that is not a bridge for Gk – 1. Denote the vertex of ek other than vk by vk 1, and extend Vπ and Eπ to Vπ : v1, v2, ......, vk, vk 1 and Eπ : e1, e2, ......, ek – 1, ek.

Step 3. Repeat step 2 until no edges remain in E.
End of algorithm.

Problem 1. Use Fleury’s algorithm to construct an Euler circuit for the graph in Figure (1).

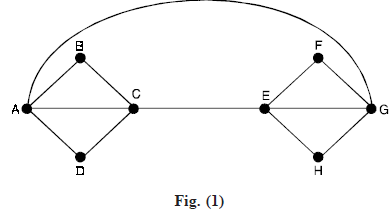
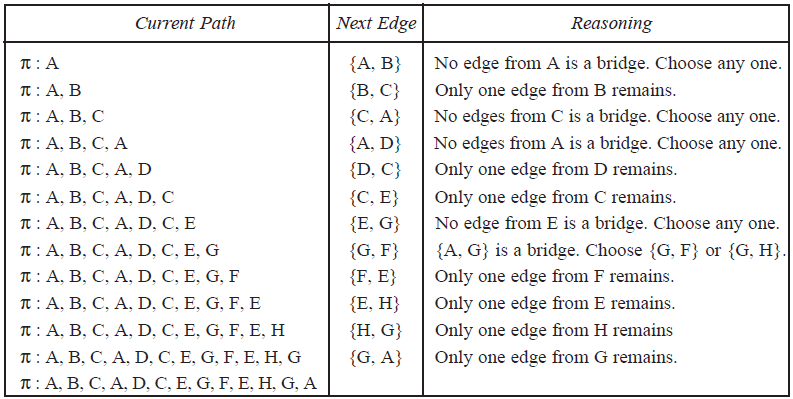
Solution. According to step 1, we may begin anywhere. Arbitrarily choose vertex A. We summarize the results of applying step 2 repeatedly in Table.

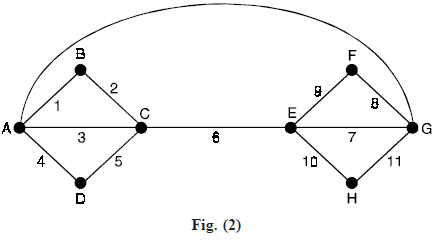
The edges in Figure (b) have been nembered in the order of their choice in applying step 2. In several places, other choices could have been made. In general, if a graph has an Euler circuit, it is likely to have several different Euler circuits.