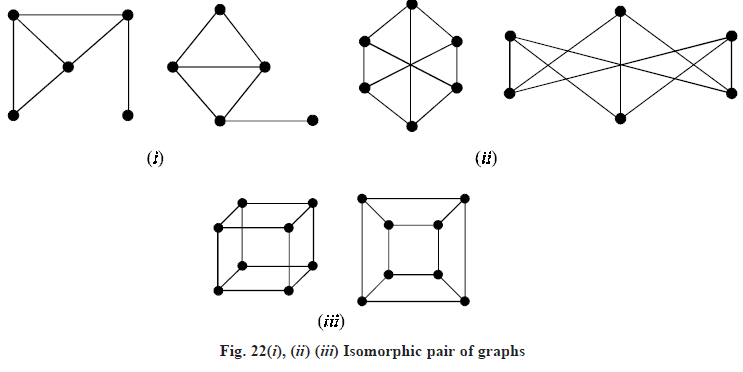
Graph Isomorphism

GRAPHS ISOMORPHISM: Let G1 = (v1, E1) and G2 = (v2, E2) be two graphs. A function f : v1 → v1 is called a graphs isomorphism if
(i) f is one-to-one and onto.
(ii) for all a, b ∈ v1, {a, b} ∈ E1 if and only if {f(a), f(b)} ∈ E2 when such a function exists, G1 and
G2 are called isomorphic graphs and is written as G1 ≅ G2. In other words, two graphs G1 and G2 are said to be isomorphic to each other if there is a oneto- one correspondence between their vertices and between edges such that incidence relationship is preserve. Written as G1 ≅ G2 or G1 = G2.

The necessary conditions for two graphs to be isomorphic are

1. Both must have the same number of vertices
2. Both must have the same number of edges
3. Both must have equal number of vertices with the same degree.
4. They must have the same degree sequence and same cycle vector (c1, ......, cn), where ci is the number of cycles of length i.

Problem 1. Construct two edge-disjoint subgraphs and two vertex disjoint subgraphs of a graph G shown below

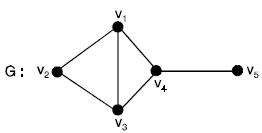
Solution.

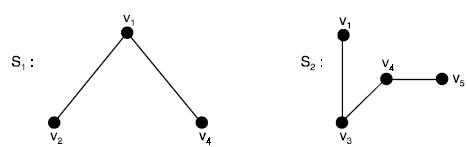
The graphs S1 and S2 are edge-disjoint subgraphs of G.

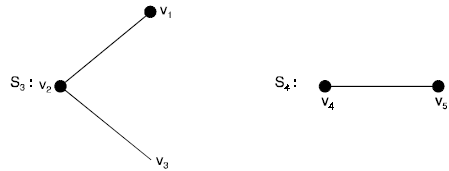
S3 and S4 are vertex disjoint subgraphs of G which are also edge-disjoint subgraphs of G.