Konigsberg's Bridge Problem

KÖNIGSBERG’S BRIDGE PROBLEM

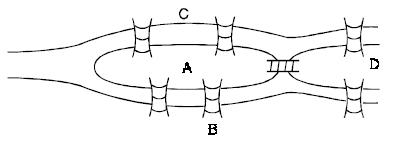
There were two islands linked to each other to the bank of the Pregel river by seven bridges as shown above.

The problem was to begin at any of the four land areas, walk across each bridge exactly once and return to the starting point.

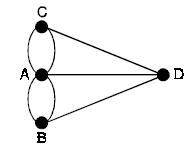
One can easily try to solve this problem, but all attempts must be unsuccessful. In proving that, the problem is unsolvable. Euler replaced each land area by a vertex and each bridge by an edge joining the corresponding vertices, there by producing a ‘graph’ as shown below :