Bipertite Graph
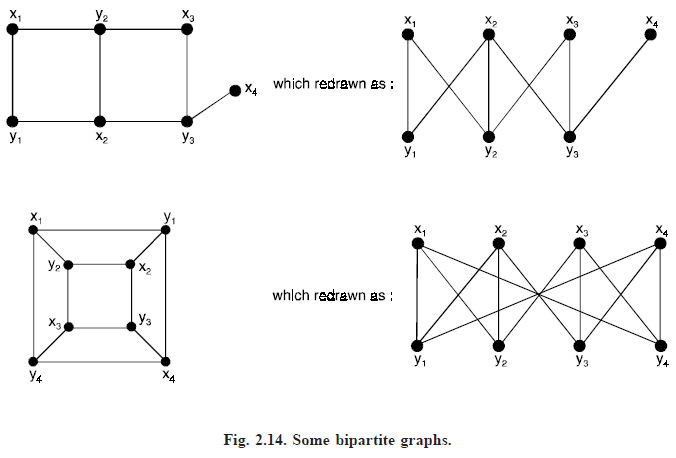
BIPARTITE GRAPH: A graph G = (V, E) is bipartite if the vertex set V can be partitioned into two subsets (disjoint) V1 and V2 such that every edge in E connects a vertex in V1 and a vertex V2 (so that no edge in G connects either two vertices in V1 or two vertices in V2). (V1, V2) is called a bipartition of G. Obviously, a bipartite graph can have no loop.
Complete bipartite graph: The complete bipartite graph on m and n vertices, denoted Km, n is the graph, whose vertex set is partitioned into sets V1 with m vertices and V2 with n vertices in which there is an edge between each pair of vertices V1 and V6. Where V1 is in V1 and V2 is in V2. The complete bipartite graphs K2, 3, K3, 3, K3, 5 and K2, 6 are shown in Figure below. Note that Kr, s has r s vertices and rs edges.
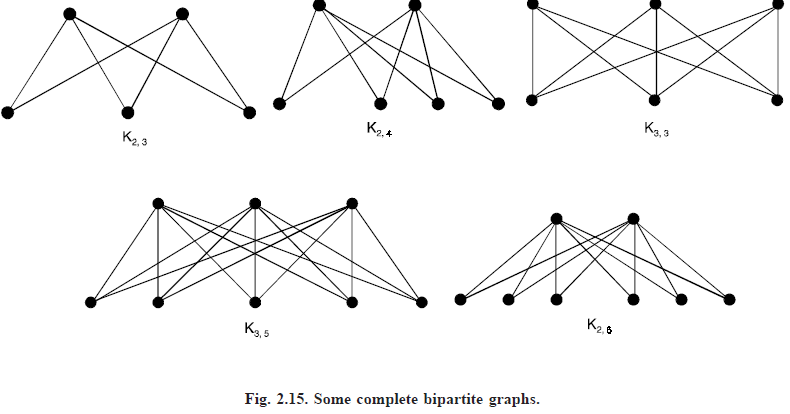
A complete bipartite graph Km, n is not a regular if m ≠ n.
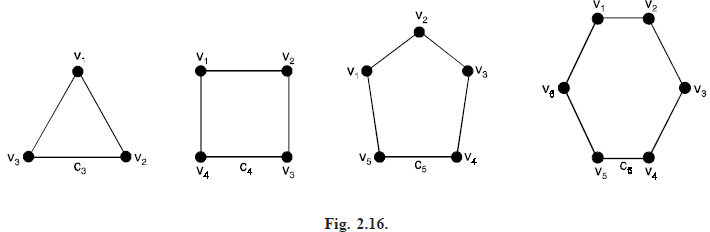
Problem 1. Show that C6 is a bipartite graph.
Solution. C6 is a bipartite graph as shown in Figure below. Since its vertex set can be partitioned into two sets V1 = {v1, v3, v5} and V2 = {v2, v4, v6} and every edge of C6 connects a vertex in V1 and a vertex in V2.
Problem 2. Prove that a graph which contains a triangle cannot be bipartite.
Solution. At least two of three vertices must lie in one of the bipartite sets, since these two are joined by two are joined by edge, the graph can not be bipartite.
Problem 3. Determine whether or not each of the graphs is bipartite. In each case, give the bipartition sets or explain why the graph is not bipartite.
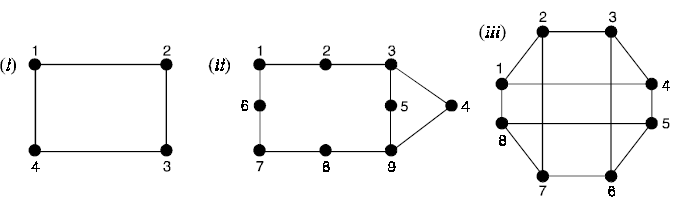
Solution. (i) The graph is not bipartite because it contains triangles (in fact two triangles).
(ii) This is bipartite and the bipartite sets are {1, 3, 7, 9} and {2, 4, 5, 6, 8}
(iii) This is bipartite and the bipartite sets are {1, 3, 5, 7} and {2, 4, 6, 8}.