Kuratowski’s Theorem
Kuratowski’s Theorem: A graph is planar if and only if it has no subgraph homeomorphic to K5 or K3, 3.
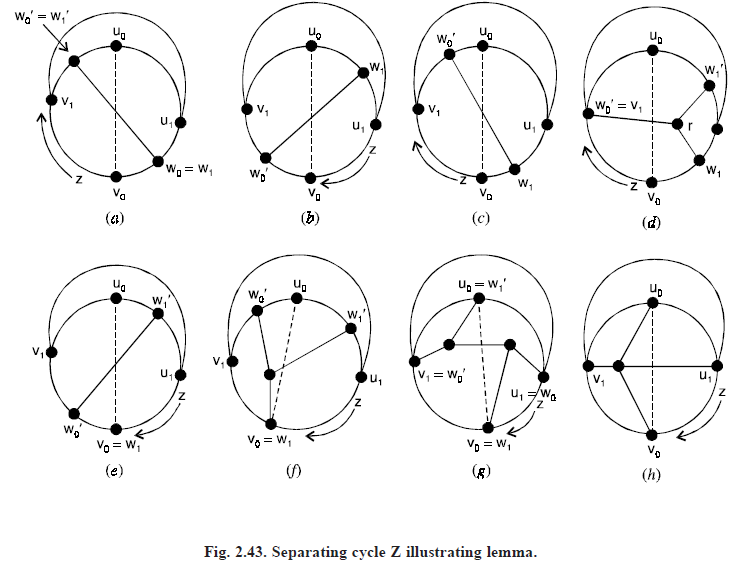
Proof. Let H be the inner piece guaranteeed by lemma (2) which is both u0 – v0 separating and u1 – v1 separating. In addition, let w0, w0′, w1 and w1′ be vertices at which H meets Z(u0, v0), Z(v0, u0), Z(u1, v1) and Z(v1, u1) respectively.
There are now four cases to consider, depending on the relative position on Z of these four vertices.
Case 1. One of the vertices w1 and w1′ is on Z(u0, v0) and the other is on Z(v0, u0). We can then take, say, w0 = w1 and w0′ = w1′, in which case G contains a subgraph homeomorphic to K3, 3 as indicated in Figure (2.43)(a) in which the two sets of vertices are indicated by open and closed dots.
Case 2. Both vertices w1 and w1′ are on either Z(u0, v0) or Z(v0, u0). Without loss of generality we assume the first situation. There are two possibilities : either
v1 ≠ w0′ or v1 = w0′. If v1 ≠ w0′, then G contains a subgraph homeomorphic to K3, 3 as shown in Figure (2.43)(b or c), dependending on whether w0′ lies on Z(u1, v1) or Z(v1, u1) respectively. If v1 = w0′ (see Figure 2.43), then H contains a vertex r from which there exist disjoint paths to w1, w1′ and v1, all of whose vertices (except w1, w1′ and v1) belong to H. In this case also, G contains a subgraph homeomorphic to K3, 3.
Case 3. w1 = v0 and w1′ ≠ u0. Without loss of generality, let w1′ be on Z(u0, v0). Once again G contains a subgraph homeomorphic
to K3, 3.
If w0′ is on (v0, v1), then G has a subgraph K3, 3 as shown in Figure 2.43(e).
If, on the other hand, w0′ is on Z(v1, u0), there is a K3, 3 as indicated in Figure 2.43(f). This Figure is easily modified to show G contains K3, 3 if w0′ = v1.
Case 4. w1 = v0 and w1′ = u0. Here we assume w0 = u1 and w0′ = v1, for otherwise we are in a situation covered by one of the first 3 cases. We distinguish between two subcases.
Let P0 be a shortest path in H from u0 to v0, and let P1 be such a path from u1 to v1, The paths P0 and P1 must intersect.
If P0 and P1 have more than one vertex in common, then G contains a subgraph homeomorphic to K3, 3 as shown in Figure 2.43(g). Otherwise, G contains a subgraph homeomorphic to K5 as in Figure 2.43(h).
Since these are all possible cases, the theorem has been proved.