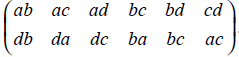Permutation Group

PERMUTATION GROUP: A collection of m permutations P = {π1, π2, ....., πm} acting on a set A = {a1, a2, ....., ak} forms a group under composition, if the four postulates of a group, that is, closure, associativity, identity, and inverse are satisfied. Such a group is called a permutation group. The number of permutations m in a permutation group is called its order, and the number of elements in the object set on which the permutations are acting is called the degree of the permutation group.

For example, the set of four permutations
{(a) (b) (c) (d), (a c) (b d), (a b c d), (a d c b)} acting on the object set {a, b, c, d} forms a permutaion group.

CYCLE INDEX OF A PERMUTATION GROUP: For a permutation group P, of order m, if we add the cycle structures of all m permutations in P and divide the sum by m, we get an expression called the cycle index Z(P) of P. For example, the cycle index of S3, the full symmetric group of degree three,

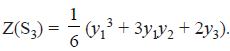
The cycle index of the permutation group is

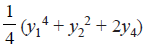
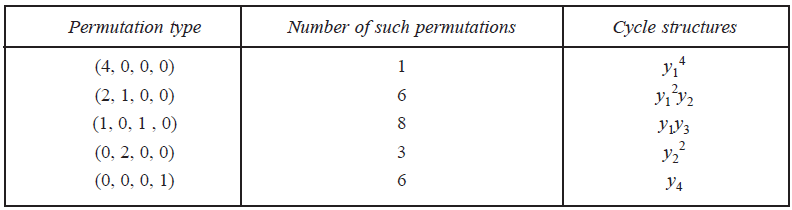
We have six permutations of type (2, 1, 0, 0) on the object set {a, b, c, d} :
(a) (b) (c d), (a) (c) (b d), (a) (d) (b c),
(b) (c) (a d), (b) (d) (a c), (c) (d) (a b).
The cycle index of S4 : Z(S4) =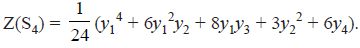

CYCLE INDEX OF THE PAIR GROUP
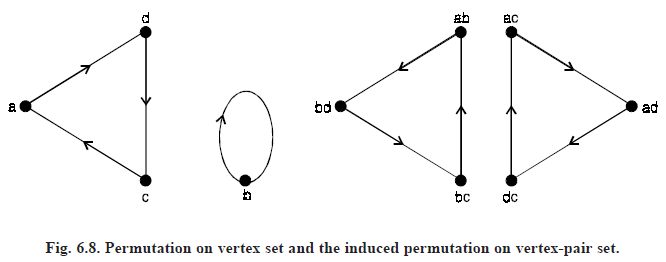
When the n vertices of a group G are subjected to permutation, the 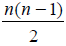unordered vertex pair also get permuted.
For example, Let V = {a, b, c, d} be the set of vertices of a four-vertex graph. The permutation
β =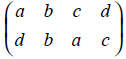
on the vertices induces the following permutation on the six unordered vertex pairs :
β′ =