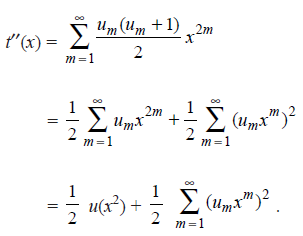Unlebeled Tree
COUNTING UNLABELED TREES The problem of enumeration of unlabeled trees is more involved and requires familiarity with the concepts of generating functions and partitions.
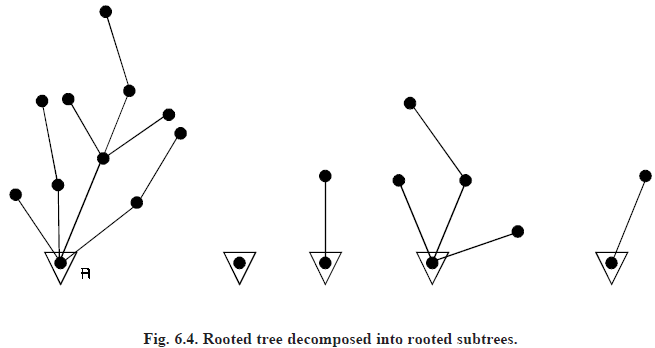
ROOTED UNLABELED TREES: Let un be the number of unlabeled, rooted trees of n vertices and let un(m) be the number of those rooted trees of n vertices in which the degree of the root is exactly m. Then
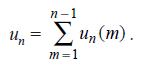
For example, In Fig. 6.4 below, an 11-vertex, rooted tree is composed of four rooted subtrees.
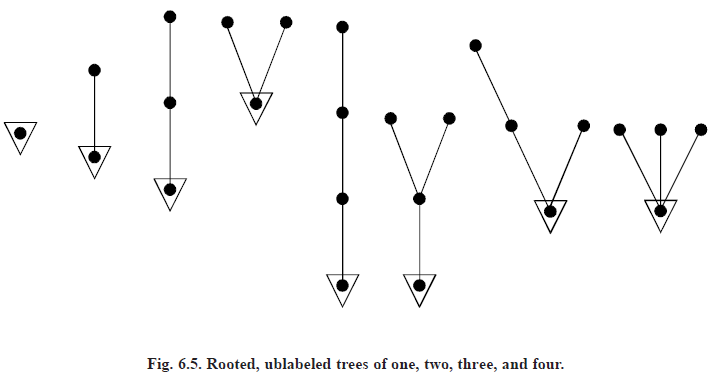
COUNTING SERIES FOR un
To circumvent some of these difficulties in computation of un, let us find its counting series, i.e., the generating function, u(x), where
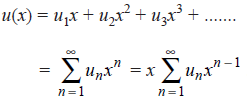
FREE UNLABELED TREES: Let t′(x) be the counting series for centroidal trees and t′′(x) be the counting series for bicentroidal trees. Then t(x), the counting series for all trees, is the sum of the two. That is t(x) = t′(x) t′′(x). Thus the number of bicentroidal trees with n = 2m vertices is given by 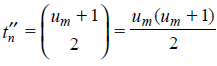
and