Rooted Lebeled Tree
ROOTED LABELED TREES: In a rooted graph one vertex is marked as the root. For each of the nn – 2 labeled trees we have n rooted labeled trees, because any of the n vertices can be made a root. Therefore, the number of different rooted labeled trees with n vertices is nn – 1.
ENUMERATION OF GRAPHS: To obtain the polynomial gP(x) which enumerates graphs with a given number P of points. Let gpq be the number of (p, q) graphs and let 
all graphs with 4 points ; g4(x) = 1 x 2x2 3x3 2x4 x5 x6.
ENUMERATION OF TREES: To find the number of trees it is necessary to start by counting rooted trees. A rooted tree has one point, its root, distinguished from the others. Let TP be the number of rooted trees with P points.
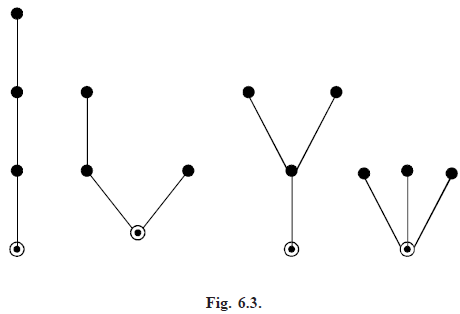
From figure 6.3 above, in which the root of each tree is visibly distinguished from the other points, we see T4 = 4. The counting series for rooted trees is denoted by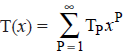 
We define tP and t(x) similarly for unrooted trees.
PARTITIONS: When a positive integer P is expressed as a sum of positive integers P = λ1 λ2 λ3 ...... λq, such that λ1 ≥ λ2 ≥ λ3 ≥ ....... λq ≥ 1, the q-tuple of called a partition of integer P.
For example, (5), (4 1), (3 2), (3 1 1), (2 2 1), (2 1 1 1), and (1 1 1 1 1) are the seven different partitions of the integer 5.
The integer’s λi’s are called parts of the partitioned number P.
The number of partitions of a given integer P is often obtained with the help of generating function.
The coefficient of xk in the polynomial
(1 x)(1 x2)(1 x3) ...... (1 xP)
gives the number of partitions, without repetition, of an integer k ≤ P.
GENERATING FUNCTIONS: A generating function f(x) is a power series
f(x) = a0 a1x a2x2 ......
is some dummy variable x. The coefficient ak of xk is the desired number, which depends on a collection of k objects being enumerated.
For example, in the generating function
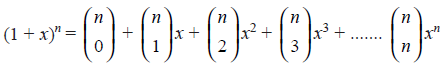
The coefficient of xk gives the number of distinct combinations of n different objects taken k at a time. Consider the following generating function :
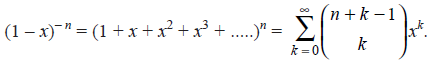
The coefficient of xk in (above equation) gives the ways of selecting k objects from n objects with unlimited repetitions.