Three Utility Problem

Three utility problem : There are three homes H1, H2 and H3 each to be connected to each of three utilities Water (W), Gas(G) and Electricity(E) by means of conduits. Is it possible to make such connections without any crossovers of the conduits with Utility Problem.

Solution:

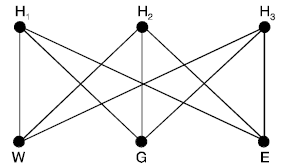
The problem can be represented by a graph shown in Figure the conduits are shown as edges while the houses and utility supply centers are vertices.
The above graph is a complete bipartite graph K3, 3 which is a non planar graph. Hence it is not possible to draw without crossover. Therefore it is not possible to make the connection without any crossover of the conduits.

Problem . Is the Petersen graph, shown in Figure below, planar ?

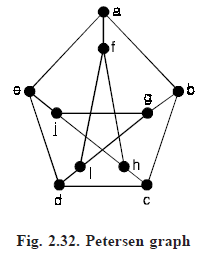
Solution. The subgraph H of the Petersen graph obtained by deleting b and the three edges that have b as an end point, shown in Figure (2.33) below, is homeomorphic to K3, 3 with vertex sets {f, d, j}

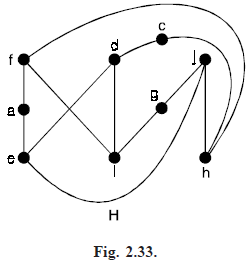
and {e, i, h}, since it can be obtained by a sequence of elementary subdivisions, deleting {d, h} and adding {c, h} and {c, d}, deleting {e, f} and adding {a, e} and {a, f} and deleting {i, j} and adding {g, i} and {g, j}.

Hence the Petersen graph is not planar.

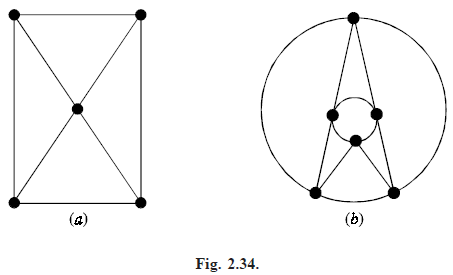
Problem . Show that the following graphs are planar :

1. Graph of order 5 and size 8
2. Graph of order 6 and size 12.

Solution. To show that a graph is planar, it is enough if we draw one plane diagram representing the graph in which no two edges cross each other. Figure (2.34) (a) and (b) show that the given graphs are planar.