Combinatorial And Geometric Graphs

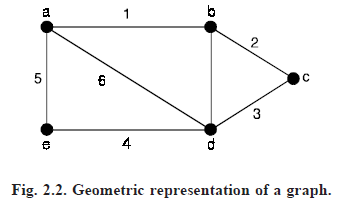
Introduction: An abstract graph G can be defined as G = (V, E, Ψ) where the set V consists of the five objects named a, b, c, d and e, that is, V = {a, b, c, d, e} and the set E consists of seven objects (none of which is in set V) named 1, 2, 3, 4, 5, 6 and 7, that is, E = {1, 2, 3, 4, 5, 6, 7} and the relationship between the two sets is defined by the mapping Ψ, which consists of combinatorial representation of the graph.

Here, the symbol 1 → (a, c) says that object 1 from set E is mapped onto the (unordered) pair (a, c) of objects from set V.

It can be represented by means of geometric figure as shown below. It is true that graph can be represented by means of such configuration.