Vertex Covering

VERTEX COVERING
A subset W of V is called a vertex covering or a vertex cover of G if every edge in G is incident on at least one vertex in W.

Trivial vertex covering: A vertex cover of a graph is a subgraph of the graph, V it self is a vetex covering of G. This is known as the trivial vertex covering.

Minimal vertex covering: A vertex covering W of G is called a minimal vertex covering if no proper subset of W is a vertex covering of G.

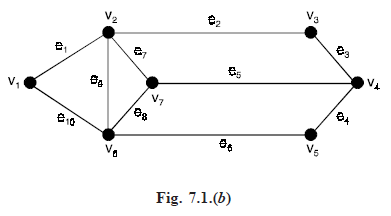
For example. In the graph shown in Fig. 7.1(b) below, the set W = {v2, v4, v6} is a vertex covering.
We check that {v1, v2}, {v1, v3}, {v2, v3}, {v1}, {v2}, {v3} are not vertex coverings of the graph.
Thus, no proper subset of W is a vertex covering. Hence W is a minimal vertex covering.

EDGE COVERING
A non empty subset S of E is called an edge covering or an edge cover of G if every non isolated vertex in G is inciedent with at least one edge in S.

Trivial edge covering: An edge cover of a graph is a subgraph of the graph, E itself is an edge covering of G. This is known as the trivial edge covering.

Minimal edge covering: An edge covering S of G is called a minimal edge covering if no proper subset of S is an edge covering of G.

For example. In Figure 7.1(b), the set S = {e1, e3, e6, e8} is an edge covering.

INDEPENDENCE: A set of points in G is independent if no two of them are adjacent.

Point independence number: The largest number of points in such a set is called the point is independence number of G and is denoted by β0 (G) or β0.

Line independence number: An independent set of lines of G has no two of its lines adjacent and the maximum cardinality of such a set is the line independence number β1 (G) or β1.
For the complete graph, β0 (KP) = 1 and β1 (KP) = [P/2].
From the above graph, β0 (G) = 2 and β1(G) = 3.