Dirichlet Integral

Dirichlet Integral:

The integral we work with here is

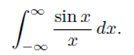
Our claim is that 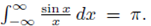We first show that the integral converges. Noting that the integrand is even, a simple parity check implies that we may work with 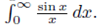If we let;

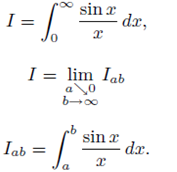
We demostrate convergence through  a simple integration by parts arguments. First note that if the upper limit of our integral I is finite, then the integral is convergent since sinx/x is continuous for all finite x. In other words for the purpose of showing convergence, we may consider sinx/x to be a continuous function is zero whose value at zero is 1. Note that,

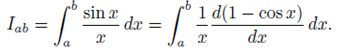
Integration by parts gives,

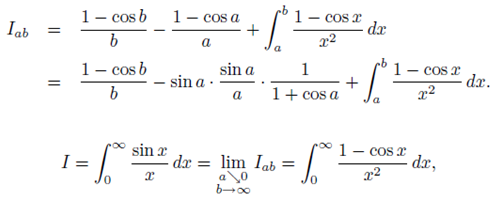
Where the last integral on the right is convergent . So having established convergence, now we calculate the value, First we state and prove the special cases of the Riemann- Lebesgue lemma. Hence this is the basic Dirichlet Integrals.