Extrema Of Function Of Several Variables

Extrema of Function of Several Variables:

Definition: We call f (a,b) a relative (local) maximum if there is an open Disk D centered at (a,b) for which f (a,b) ≥ f (x,y) for all (x,y) ∈ D. Similarly f (a,b) is called a relative (local) minimum there is an open Disk D for which f (a,b) ≤ f (x,y) for all (x,y) ∈ D. In either case f (a,b) is called a relative (local) extremum of f.

Definition: The point (a,b) is called a critical point of f if (a,b) is in the domain of f and either $\nabla \!\,$ f = 0 or is undefined. Note that $\nabla \!\,$ f = 0 if f_x(x,y) = 0 and f_y (x,y) = 0. $\nabla \!\,$ f doesnot exist.

Theorem: If f (x,y) has a local extremum at (a,b) then (a,b) must be a critical point of f. However, if a point is a critical point it may not be a relative maximum or relative minimum. It could be saddle point. Look at (0,0) on the graph of z = x² - y²

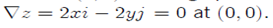But (0,0) is not a relative extremum of z.

Theorem: Suppose that f (x,y) has continuous 2nd order partial derivatives in some open disk containing the point (a,b) and that f_x (a,b) = f_y (a,b) = 0.

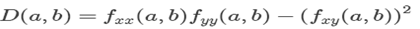is called the Discriminant.

Examples: Consider the functions f (x,y) = 16 - x² - y². Locate all critical point and classify them.

Solution:

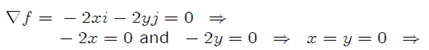
The only critical point is (0,0).

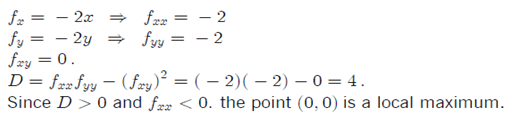
What about the functions f (x,y) = x² y².

fx = 2x and fy = 2y and again the only critical point is (0,0).

Then f_xx = f_yy = 2 and fxy = 0.

At (0,0), D = 4 but f_xx > 0 ⇒ (0,0) is local minimum.