Indeterminate Forms

Indeterminate Forms:

If f (x) and g (x) are two functions, then we know that

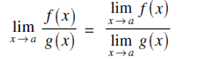
If Then the expression 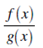is said ro be have the indeterminant form 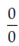, at x = 0

If 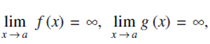then 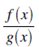is said to have indeterminant form 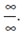Hence the other indeterminant forms are

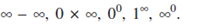
Indeterminate Form 0/0:

Here we shall give a method called L' Hospital's Rule to evaluate the limits of the expression which take the indeterminant form;

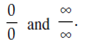
L's Hospital's Theorem

Let f (x) and g (x) be two functions such that

1.

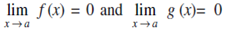
2. 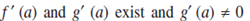Then

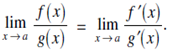
Proof : Suppose f (x) and g (x) satiesfy the conditions of Cauchy's mean value theorem in the interval [a,x]. Then we have

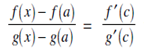where c lies between a and x i.e a<c<x

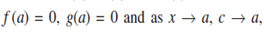we get;

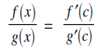
Hence,

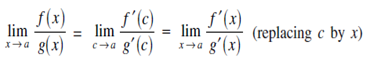
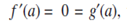Then this theorem can be extended as follows:

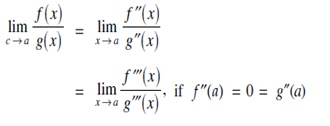
and so on.