Maxima And Minima Of Function Of Two Variables
Maxima And Minima of Function of Two Variables:
Maximum Value of Function:
A function f (x,y) is said to have a maximum point (a,b), if these exists a neighbourhood N of (a,b) such that;
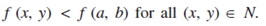
Minimum Value of Function:
A function f (x,y) is said to have a minimum point (a,b), if these exists a neighbourhood N of (a,b) such that;
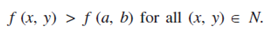
Necessary and Sufficient Conditions for Maxima and Minima:
The necessary conditions for a functions f (x,y) to have either a maximum and minimum at a point (a,b) are fx (a,b) = 0 and fy (a,b) = 0. The point (x,y) where x and y satiesfy fx (x,y) = 0 and fy (x,y) = 0 are called the Stationary or the Critical value of the functions.
Suppose (a, b) is a critical value of the functions f (x,y). Then fx (a,b) = 0 and fy (a,b) = 0. Now denote:
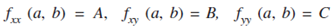
1. Then. the functions f (x,y) has maximum at (a,b) if AC - B2 > 0 and A < 0.
2. The functions f (x,y) has minimum at (a,b) if AC - B2 > 0 and A > 0.
Maximum and Minimum value of functions are called the Extreme value of the function.
Working Rule to find the maximum and minimum value of function f (x,y):
1. Find fx (x,y) and fy (x,y).
2. Solve the equations fx (x,y) = 0 and fy (x,y) = 0.
3. Then find fxx (x,y), fxy (x,y) , fyy (x,y).
4. Then A = fxx (a,b) , B = fxy (a,b), C = fyy (a,b).
5. If AC - B2 > 0 and A < 0 the f has maximum at (a,b).
6. If AC - B2 > 0 and A > 0 the f has minimum at (a,b).
7. If AC - B2 < 0, then f has neither a maximum nor a minimum at (a,b) . The point (a,b) is called Saddle Point .
8. If AC - B2 = 0, further investigation is necessary.