Theorem Of Line Integral

Theorem of Line Integral:

One way to write the Fundamental Theorem of calculus is:

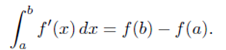
That is to compute the integral of derivatives f' we need only compute the value of f at the end points. Something similar is true for line integral of a certain form.

Theorem: Fundamental Theorem of Line Integral- Suppose  a curve C is given by the vector r (t), with a = r (a) and b = r(b). Then

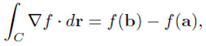
provided that r is sufficciently nice.

Proof: We write 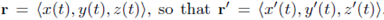Also we know that 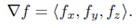Then

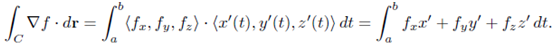
By the chain rule 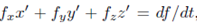where f is the context mean 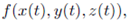a function of t. So we have,

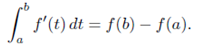
In this context 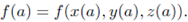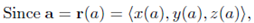we can write f(a) = f(a) - this is a bit of cheat, since we are simultanously using f to mean f(t) and f(x,y,z) and since 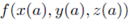. Doing the same for b is we get;

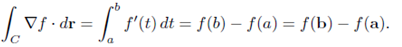
This theorem is called the Fundamental Theorem of Calculus, says roughly that if we integrate a "derivatives-like function" the results depend only on the value of the original function (f) at the end points.