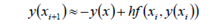Euler Method
Euler Method:
Recall the Differential Equation we get:
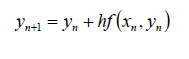
where n is the step count (n = 1,2,3....) and xn = x0 nh.
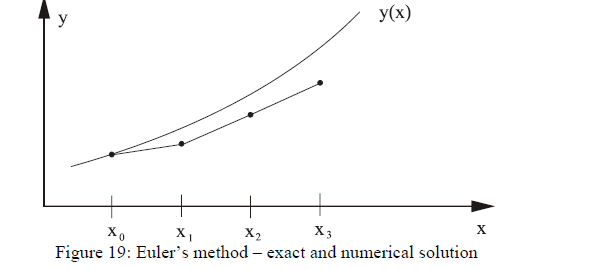
In figure 19 the curve y (x) represents the exact (but unknown) solution that we are seeking. We are given the value y0 = y (x0). And this value is used to calculate the gradient of the curve at x0. We then represent the curve by the straight line through the point (x0, y0) with a gradient f(x0, y0). The equation of this line is:
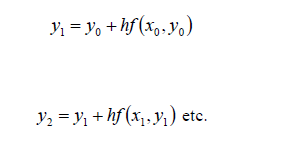
Clearly the solutions may be improved by reducing the step size h. Although it may need to be very small to give sufficiently accurate solutions. Also, Euler’s method can sometime suffer from instability – where small errors in the initial values get amplified by the solution method. It is possible to formally derive Euler’s method from Taylors theorem, recall equation 28 ignoring the third derivative and writing in terms of y (x) instead of f (x).
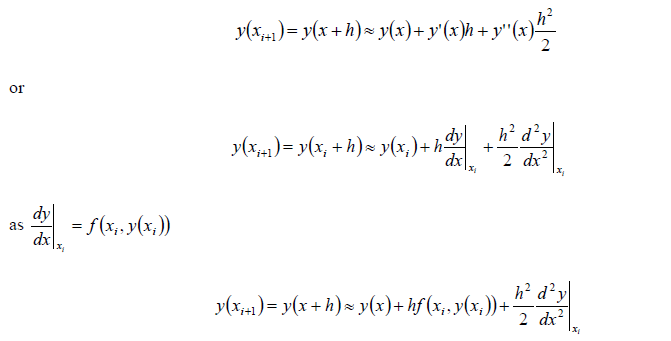
The equation can be rewritten:
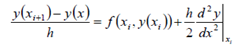
If we ignore the second derivative which will be small for small h, then Euler Method is:
