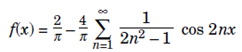Half Range Fourier Series

Half Range Fourier Series:

It is often convenient to represent a given function as a Fourier series which contains only cosine terms or only sine terms, as in the initial examples. If f(x) is piecewise continuous on [0, π ], it can be extended to [–π , 0] as either an even function or as an odd function.

Then f is periodically extended to the whole real lines as a 2π - periodic functions by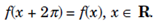

Let f(x) be a piecewise smooth function given on the intervals [0 ,π] and extended to [-π, 0] as an even functions. Thats is , f(x) = f (-x), x ε [-π, 0]. Then the periodic extensions to R, is piecewise smooth and has Fourier series.

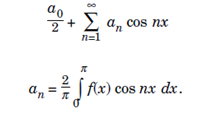
Similarly extending f(x) to [-π, 0] as an odd function and periodically to R. tha extension has Fourier series;

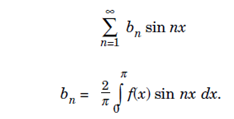
The fourier series 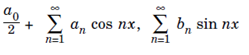are known as Half-Range series for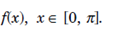

Examples: Let f (x) = sinx, x ∈ [0, π]. Extends f to [-π, 0] as an even functions.

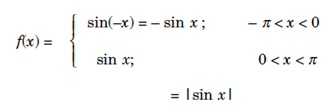
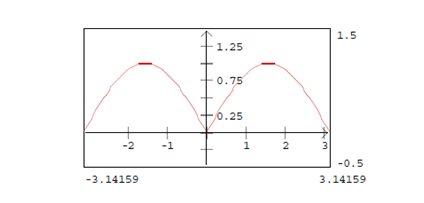
The half - range Fourier series of f is given by;