Fourier Coefficients
Fourier Coefficients:
Given a T-periodic signal v, it is possible to compute the Fourier coefficients of (4) with the following equations:
a0 is referred to as the DC component of the signal, and ak and bk are the Fourier coefficients for the kth harmonic. Notice that a0 is nothing more than the average of the function computed over one period (the interval [0,T]). Furthermore, notice that ak and bk are nothing more than the average of the function over one period after it has been multiplied by either cos(2πkt/T) and sin(2πkt/T).
Example: Calculate the Fourier coefficients of
This is actually written in the form of a Fourier series, so we can determine the Fourier coefficients by inspection. In particular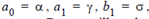 
with all the fourier coefficients being identically equal to zero. But we will go through the process of computing them using (10) - (12) to familiarize ourselves with the process. Lets start by calculating the DC components:
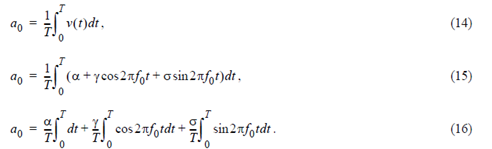
Notice that the first term integrals 1 from 0 to T. getting T, and then multiplies by α over T, giving α. The second and third terms integrate a cosine and sine functions over one complete periods, which gives 0. Thus a0 = α
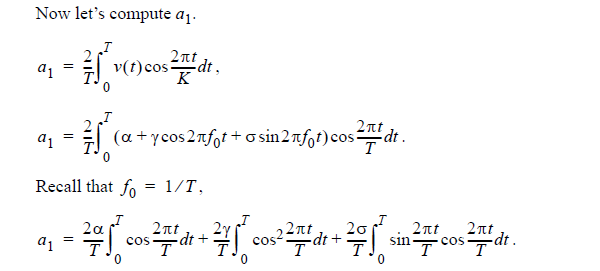
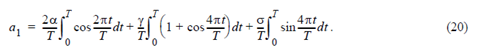
Here the second term evaluates to 1 while the first, third and fourth terms integrate a cosine and sine functions over either one or two full periods and so are 0. Thus a1 = δ as expected.
and so on calculation goes on.