Fourier Series
Fourier Series:
The basic idea of the Fourier series is that any periodic waveform can be represented with a sum of harmonically related sinusoids. Let’s break this statement down. First, a waveformis a function of time. A waveform is periodic if it repeats itself identically after a period of time. Let the period be denoted T. Then mathematically, a T-periodic waveform v satisfies
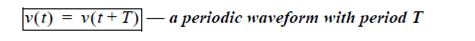
for all t. To make things simpler, let’s further assume that v is a continuous function of time. The Fourier series of this waveform can be written as:
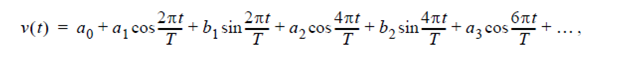
This can be written as:

where b0 is assumed to be 0. This is an infinite series, and in order for it to converge and both must go to 0 as k goes to infinity. In other words there must be some value of K beyond which the contributions of |ak| and |bk| become negligible for k > K. This implies that if the sum only includes a finite number of terms it becomes an approximation for v and the accuracy of the approximation improves as K increases.
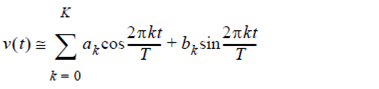
for some K. This point is illustrated in Figure 2, which shows a square wave being approximated by a finite Fourier series. The sum is shown for the cases in which K equals 1, 3, 5, and 7. You can see that the series more closely approximates the function as K increases.
The fundamental frequency f0 is defined as the reciprocal of the period,

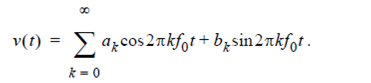
You will notice that the sinusoids that make up the sum are all at frequencies that are integer multiples of the fundamental frequency. These frequencies are referred to as harmonics of the fundamental frequency.