Fourier Series Of Functions With Arbitrary Periods

Fourier Series of Functions with Arbitrary Periods:

So far, we’ve worked with 2π-periodic functions for convenience. Similar results exist for functions having any period. These results can be obtained in a similarmanner. However, there is an easier way, one calculus II students are familiar with: substitution. One way to obtain a new series representation is to perform a substitution in a known series. Suppose that f is a function with period T = 2p > 0 for which we want to find a Fourier series. In other words f (x 2p) = f (x). If we let t = πx / p and we define:

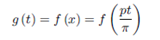
Then g has period 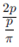that is 2π. So, g has a fourier series representation;

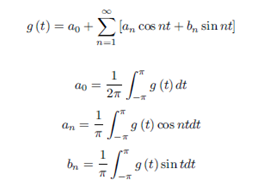
Using the substitution t = πx/p, we obtain

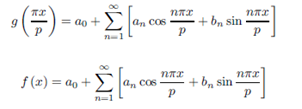
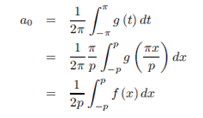
So, we have the following;

Theorem-27 Suppose that f is a 2p - periodic function piecewise smooth function. The fourier series of ff is given by;

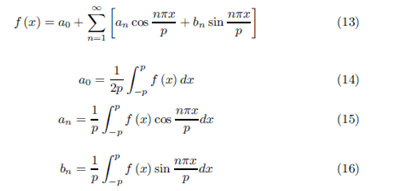
The Fourier series converges to f (x) if f is continuous at x and to 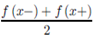otherwise f is either even or odd.