General Interval

General Interval: General Intervals of Fourier Series are given as:

The theory of Fourier series can be expanded to include functions which have arbitrary period. Let f : R→R have period 2l > 0 . That is f (x 2l) = f (x), xεR. Also define Φ: R→R by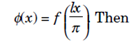

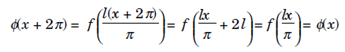
So Φ has period 2π. Applying the result earlier result to , result in the Fourier series.

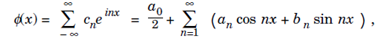
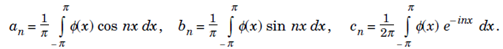
The change of variable y = lx/π leads to;

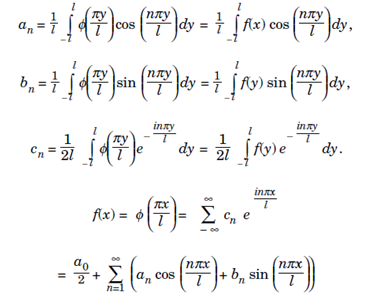
is the Fourier series of a 2l-periodic function f.

It follows from the above calculations that if f(x) is even functions on [l,-l], its fourier series contain no sine terms and is of the form;

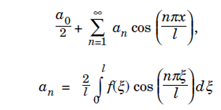
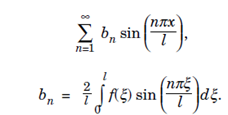
A function f (x) defined on an interval [0,l] can be extended to [l,-l] either as an even or an odd functions and be extended periodically with period 2l to real line. The fourier series of such functions are half-range expansions on [0,l] and contain no sine terms in the case of an even extensions or no cosine terms of an odd extensions.