Ordinary Differential Equation
Ordinary Differential Equation:
Higher order differential equations with constant coefficients – Method of variation of parameters – Cauchy’s and Legendre’s linear equations – Simultaneous first order linear equations with constant coefficients.
The study of a differential equation in applied mathematics consists of three phases.
(i) Formation of differential equation from the given physical situation, called modeling.
(ii) Solutions of this differential equation, evaluating the arbitrary constants from the given conditions, and
(iii) Physical interpretation of the solution.
Higher Order Linear Differential Equation With Constant Coefficient:
General form of Linear differential equation of nth order with constant coefficients is:
![]()
Where X is a function of x and a1,a2....,an are constant and is called Linear Differential Equations of nth order with constant coefficients. Since the highest order of the derivative appearing in (1) is n, it is called a differential equation of nth order and it is called linear. Using the familiar notation of differential operators:
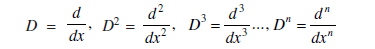
Then (1) can be written in the form
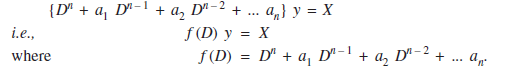
Here f (D) is a polynomial of degree n in D
If x = 0, the equation
f (D) y = 0
is called a homogeneous equation. If x ≠ 0 then the Eqn. (2) is called a non-homogeneous equation.
(1) The general form of the differential equation of second order is:
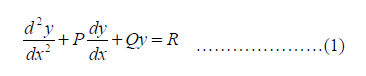
Where P and Q are constant and R is a function of X or constant.
(2) Differential Operators:
The symbol D stands for the operation of differential
