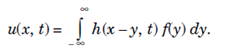Heat Conduction Equation

Heat Conduction Equation:  The heat equations,

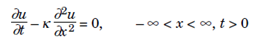
For u (x, t) a function of two variables, with initial conditions

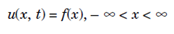
For f ∈ L¹ (R), for continuous and bounded, can be solved using Fourier transform. Taking transforms in the variable x,

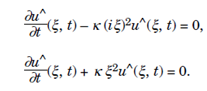
Solving the first order ordinary differential equations,

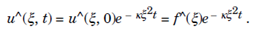
Now 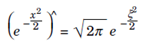using the dilation property of Fourier Transforms

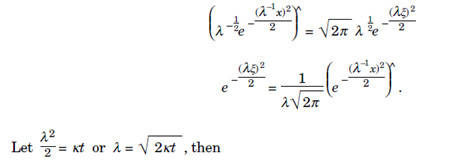
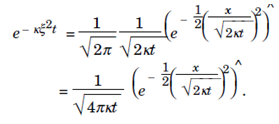
Therefore from the convolution theorem since,

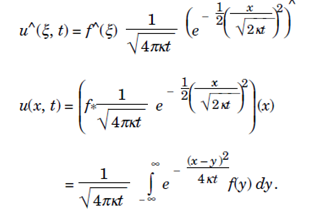
Hence, Heat Function is: