Laplace Transform
Laplace Transform:
The Laplace transform method is used for solving the differential equations with initial and boundary conditions. The advantage of this method is that it solves the differential equations with initial conditions directly without the necessity of first finding the general solution and then evaluating the arbitrary constants using the initial conditions. In particular, this method is used in problems where the driving force (mechanical or electrical) has discontinuities for a short time or is periodic. In this unit we study the basic concepts of Laplace transforms and its applications to solve the differential equations arising in mechanics, electrical circuits and bending of beams.
Definition:
Let f ( t ) be a real valued function defined for all t ≥ 0. Then the Laplace transform of f ( t ) denoted by L{ f ( t ) } is defined by:
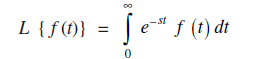
where s is a real or a complex number. In the integral on the right hand side (1) exists, it is a function of s and is usually denoted by F (s). Here s is called the parameter.
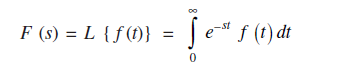
Properties of Laplace Transformation:
Let f(t) and g(t) are two function defined for all positive value of t and k is a constant the:
![]()
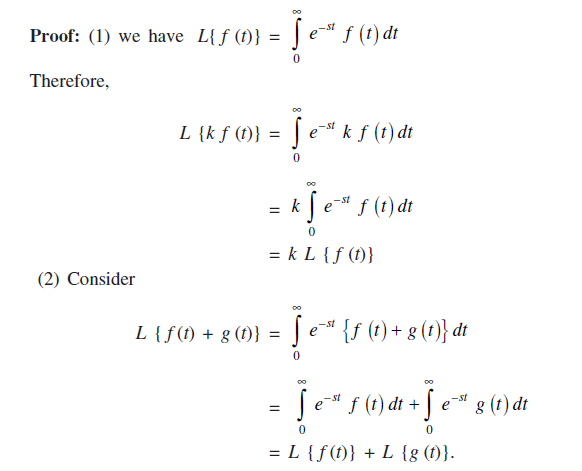
Laplace Transformation is divided into following subgroup: