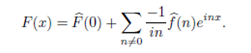Integration Of Fourier Series

Integration of Fourier Series:

The following is a cosequence of the fundamental theroem of calculus:

Preposition 6: If f : [a ,b]→C is sectionally contineous, then

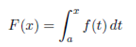
is contineous. Furthermore, F is differentiable at each point of [a, b] except perhaps at the points of discontinuity of f, where it has right and left derivatives.

Suppose that f : [0, 2π] → C is sectionally continuous. Then it is integrable on [0, 2π] so that we can compute its Fourier series. Let this be;

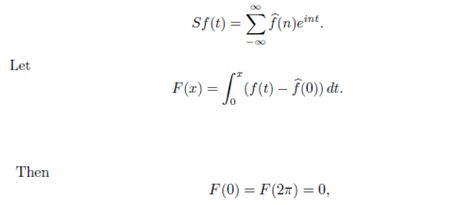
and together with the proposition above it follows that F satiesfies a Lipschitz condition on [0, 2π]. Hence the Fourier series of F converges uniformly to the function F. To compute it we use integration by parts. If n ≠ 0.

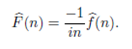
Note that you have to justify the validity of the integration by parts because F may not have continuous derivatives on [0, 2π].

Hence,