Laplace Transform Of Periodic Function

Laplace Transform of Periodic Function:

A function f (t) is said to be periodic function with periods α > 0, if f (t a) = f (t)

Theorem: if f (t) is a periodic function of period α > 0, then

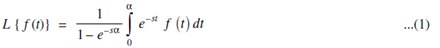
Proof:
   

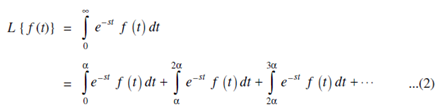
Substitute, t = u a in the second integral;

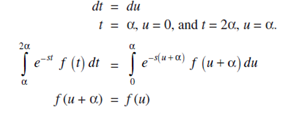
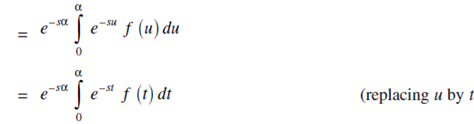
Similarly by substituting t = u 2α in the 3rd integrals, we get;

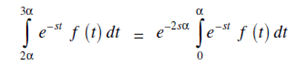
∴ equation (2) reduces to;

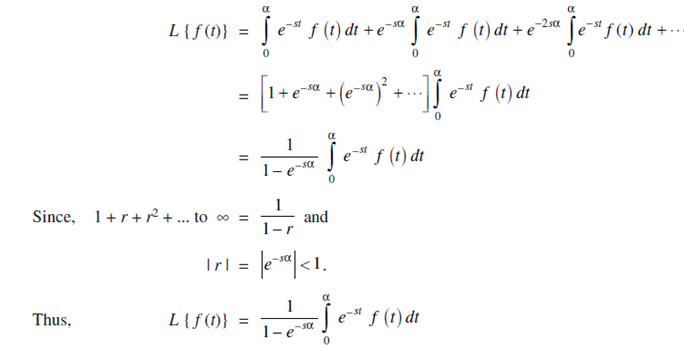
This completes the proof of the theorem.