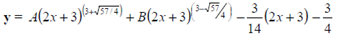Legendre Linear Equation

Legendre Linear Equation:

It is the Form: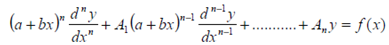

Where A₁,A₂,..........,A_n are constants. It can be reduced to linear differential equation with constant coefficients.

By taking: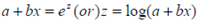

Consider:
             

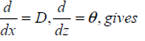
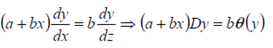
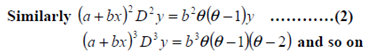
Substitue (2) in (1) gives: the linear differential equation of constant coefficients.

Examples: Solve (2x 3)²y'' - (2x 3)y' - 12y = 6x

Solution: This is Legendre's linear equation:

            (2x 3)²y'' - (2x 3)y' - 12y = 6x................(1)

            Put z = log (2x 3), e^z = 2x 3

            (2x 3)D = 2θ

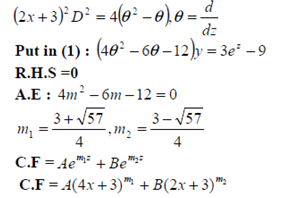
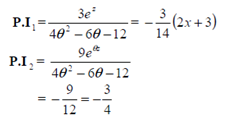
Solution is: