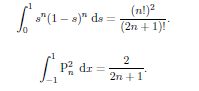Orthogonality Of Legendre Polynomials
Orthogonality of Legendre Polynomials:
The differential equation and boundary condition satiesfies by the Legendre Polynomials forms a generalized system where the boundary condition amount to insisting on regularity of the solutions at the boundaries). They should therefore satiesfies the Orthogonality Relations.
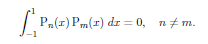
If Pn and Pm are solutions of Legendre's equations then;
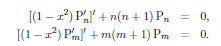
Integrating the combination Pm (C.5) - Pn (C.6) gives
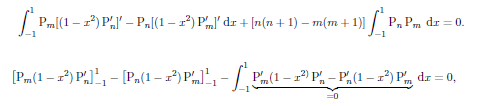
as Pm,n and their derivatives are finite at x = ± 1. Hence, if n ≠ m.

Generating Functions for Legendery Polynomials:
We consider afunction of two variables G( x , t ) such that,
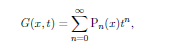
So that legendery polynomials are the coefficients in the Taylor Series of G( x , t ) about t = 0. Our first task is to identify what the function G( x , t )actually is.
What is 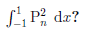
We can evaluate this integral using Rodrigue's formula. We have
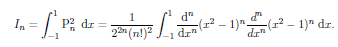
Integraing by parts give;
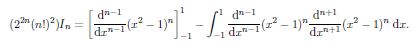
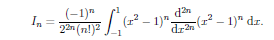
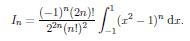
The complition of this arguments is left as an exercise. One way to proceed is to use the transformation s = (x 1)/2 to transform the integral and then use a reduction formula to show that;