Properties Of Legendre Polynomials

Properties of Legendre Polynomials:

The Legendre Polynomials are the everywhere regular solutions of Legendre’s Equation,

                     (1 − x²)u′′ − 2xu′ mu = [ (1 − x²)u′ ] ′ mu = 0,

which are possible only if

                                           m = n(n 1), n = 0, 1, 2,……

We write the solution for a particular value of n as P_n(x). It is a polynomial of degree n. If n is even/odd then the polynomial is even/odd. They are normalized such that P_n(1) = 1.

                                            P₀(x) = 1,

                                            P₁(x) = x,

                                            P₂(x) = (3x²− 1)/2,

                                            P₀(x) = (5x³− 3x)/2.

Rodrigue’s Formula:

They can also be represented using Rodrigue’s Formula:

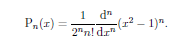
This can be demonstrated through the following observations which are given as:

1. It’s a Polynomial.

2. it take the value 1 at 1 if,

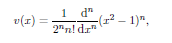
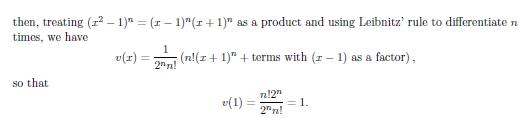
3. It satiesfies the equation.

Finally;

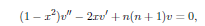
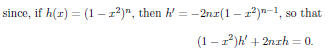
Now differenciate n 1 times, using Lebnitz to get;

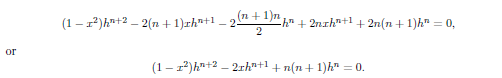
As the equations is linear and 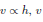satisfies the equation also.