Period Of Multiple Function

Period of Multiple Function:

If f and g are periodic of period p then so is f g

Proof : Denote f g by h want h (x p) = h (x)

h (x p) = f (x p g(x p))

f (x) = g (x)

h (x) Where h is periodic of periods p.

If f is a periods of p then the graph of f repeats itself every p units.

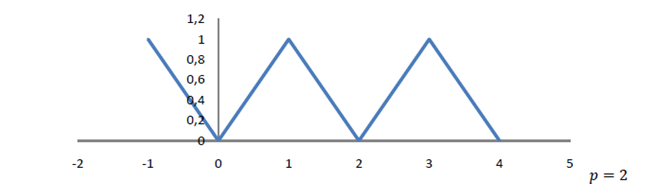
Therefore if we know the curve of periodic function on 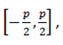Then we can draw the entire graph.

Example:

If f is a periodic of period p then;

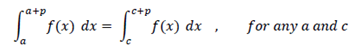
Fourier Series:

Our purpose is to approximate periodic functions by sine and cosine. We define further Fourier Series of the periodic function f (x) by:

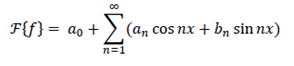
Fourier Coefficients a₀, a_n and b_n can be obtained by Euler Formulas.