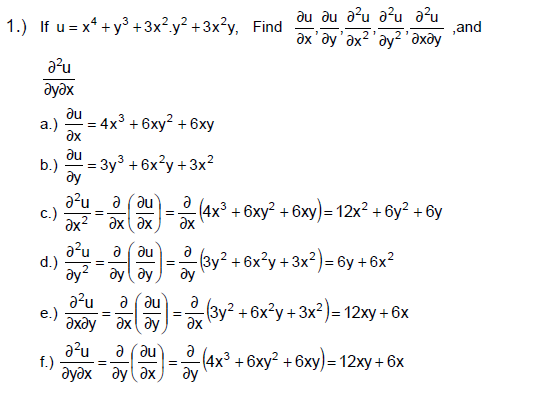Partial Differentiation

 Partial Differentiation:

Functions of two or more variables: In many applications, we come across function involving more than one independent variable. For example, the area of rectangle is a function of two variables, the length and breadth of the rectangle.

Definitions: Let u = f (x , y)  be a function of two independent variables x and y. The derivatives of u with respect to x varies and y remains constant is called the partial derivatives of u with respect to x is and is denoted by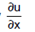

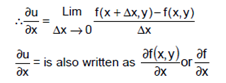
Similary when x remains constant and y varies, the derivatives of u with respect to y is called the partial derivatives of u with respect to y and is denoted by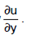

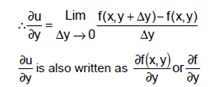
Secons order partial derivatives: In general 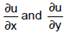are also function of x and y. They can be further differentiated partially w.r.t x and y as follows:

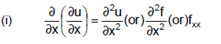
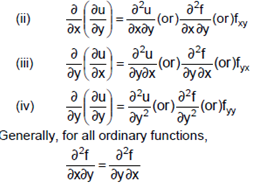
Example: