Binomial Distribution
Binomial Distribution:
The binomial distribution1 is a discrete probability distribution which is used when there are exactly two mutually exclusive outcomes of trials. These outcomes are appropriately labeled success and failure. This is used to obtain the probability of observing x successes in n trials, with the probability of success on a single trial denoted by p. The binomial distribution assumes that p is fixed for all trials. Consider a random experiment which has two possible outcomes success and failure. The probability of success in each trial is p and remains same for all n trials. The trials are independent. Let X is a random variable which represents the number of successes in n trial. Then X has n values named as 0 success, 1 success, 2 successes, ..., n successes., i.e.
X = x : 0,1,2,3, ...,n
This distribution is associated with the name of James Bernoulli (1605-1705) and was published in 1713. It is also called as Bernoulli distribution in his honor. with probability of x successes as;
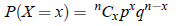
where q = 1 − p: the probability of failure in a single trial. If the random experiment of n independent trials is repeated N time, then the expected number of trials showing a success is
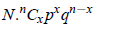
The set of the numbers of success x along with the corresponding probability is known as Binomial Probability Distribution. The set of the number of successes along with the corresponding theoretical frequencies is called Theoretical Binomial Distribution with parameters n and p.
Assumptions of Binomial Distribution:
Binomial distribution is based on the following assumptions
1. The Bernoulli trials are independent.
2. The number (n) of trial is finite and fixed.
3. The trials are repeated under identical conditions.
4. There are two mutually exclusive possible outcomes of each trial which are referred to as ‘success’ and ‘failure’.
5. In a single trial probability of success is p and the probability of failure is q where p q = 1. The probability of success (and therefore for failure) remains same for each trial.
Example-1: If on an average one ship in every ten is wrecked, find the probability of arrival of at least 4 ships safely out of 5 ship expected to arrive.
Solution: Given that one ship out of 10 is wrecked. i.e., 9 are safe.
Probability of safe ship arriving: = 9/10
Here, we have to compute probability of arriving at least 4 ships safely out of 5 expected to arrive. Here n is 5. Since we need at least 4, it means there are either 4 safe ship or more than that. Thus here x has two values 4 and 5.
