Difference Operators

Difference Operators:

So far we have studied the operators Δ, and δ. Here we will discuss some more operators which play a vital role in numerical analysis.

1. Shifting Operator:

If h is the interval of differencing in the argument x then the operator E is defined as

Sometimes it is also called translation operator due to it results value of the function for the next argument. Furhter we observe that;

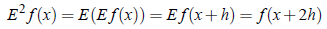
In general, for all integral values of n

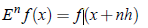
2. The D Operator:

The differential coefficient of y with respect to x is denoted by Dy, where D ≡ d/dx. Here D is called as differential operator or simply operator D. We may denote nth derivative of y with respect to x as Dⁿy. Here Dⁿ is called nth differential operator.

3. The Mean Operator:

The mean operator is denoted by μ and is defined as;

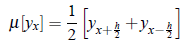
Some Important Relations:

The shift operator E is fundamental operator. All other derivatives may be derive from it. In this section we discuss some representation of other operators in terms of E. We have;

Which implies Δ ≡ E − 1, i.e.

                      E ≡ 1 Δ

Similarly for the backward operator, we have

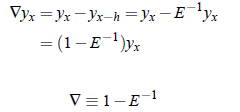
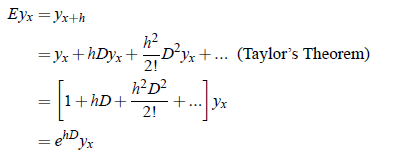
By using relation above and rearranging, we get

                              Δ ≡ e^hD −1.