Lagranges Interpolation

Lagranges Interpolation:

Let f (x₀), f (x₁), ..., f (x_n) be n 1 entries of a function y = f (x), where f (x) is assumed too be polynomial corresponding to the arguments x₀, x₁, ...,x_n.

The polynomial f (x) may be written as;

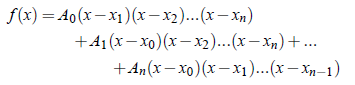
where A₀,A₁, ...,A_n are constants to be determined.

Putting x = x₀

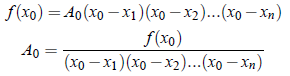
Putting x = x₁

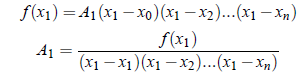
Similarly,

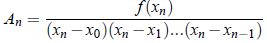
Hence, on substituting the constants values, we get

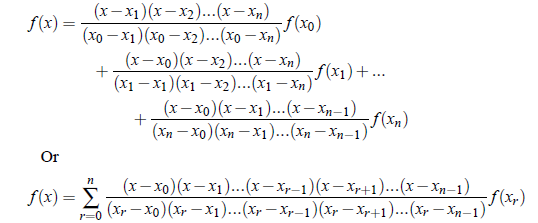
This result is known as Lagrange’s Interpolation Formula.