Newton Raphson Method
Newton Raphson Method:
When an approximate value of a root of an equation is given, this method is used to obtain better and closer approximation to the root. Let x0 be an approximation of a root of the given equation f (x) = 0, Let x1 = x0 h be the exact approximation of the root. Then f (x0 h) = 0.
By Taylor’s theorem, we have
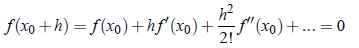
Since h is small, we can neglect second, third and higher degree terms in h and thus we get
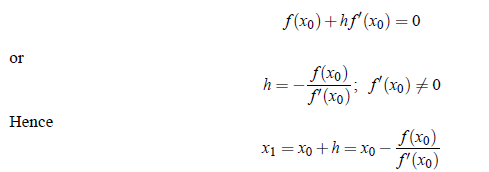
We may iterate the process to refine the root. In general, we may write
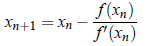
This result is known as Newton-Raphson formula.
Example: Solve sinx = 1 x3 using Newton-Raphson Method.
Solution: Let f (x) = sin x − 1 − x3, then f ′(x) = cos x − 3x2. Then Newton-Raphson formula for this problem reduces to;
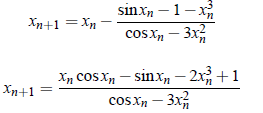
Now, since f (−1) < 0 and f (−2) > 0, root lies in between −1 and −2. Let x0 = −1.1 be the initial approximation. then successive iteration from above equations are;
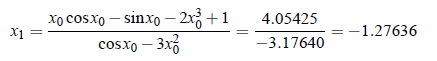
Similarly, x2 = −1.249746, x3 = −1.2490526, x4 = −1.2490522. In x2 and x3 6 decimal places are same. i.e. approximated root up to six decimal place is -1.249052.