Newtons Cotes Quadrature Formula

Newton’s Cotes Quadrature Formula:

Let 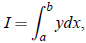where y = f (x) takes the values y₀, y₁, y₂, ...,y_n for x₀, x₁, x₂, ...,x_n. Let us divide the interval (a,b) into n equal parts of width h, so that;

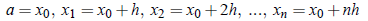
Then

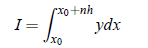
On substituting x = x₀ rh, so that dx = hdr, we get

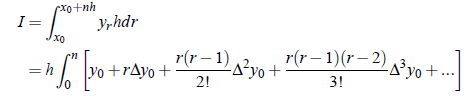
Now on integrating term by term, we get

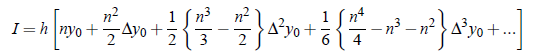
Above Equation is known as Newton Quadrature Formula, which is also called as general qudrature formula.

Trapezodial Rule:

Setting n = 1 in the above equations, we obtain

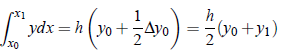
For susequent intervals, similarly,

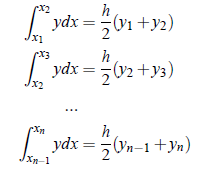
On adding all the above results,

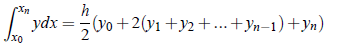
which is known as Trepezodial Rule.