Newtons Divided Difference Interpolation Formula
Newton’s Divided Difference Interpolation Formula:
The Lagrange’s formula has the drawback that if another interpolation values were inserted then the interpolation coefficients are required to be recalculated. This labour of recomputing is saved by using Newton’s general interpolation formula which is based on divided differences.
Divided Difference:
If (x0, y0), (x1, y1), (x2, y2), ... be given points, then the first divided difference for the argument x0, x1 is denoted as [x0, x1] defined as
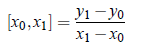
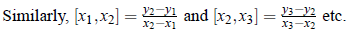
The second divided difference for x0, x1, x2 is defined as;
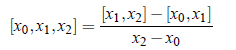
The third divided difference for x0, x1, x2 is defined as;
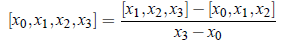
and so on. Here it is notable that we can write [x0, x1] as
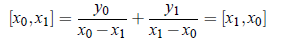
which shows symmetry in divided differences. Thus, the divided are symmetrical in their arguments, i.e. independent of the order of the arguments.
Newton’s General Interpolation Formula:
Let y0, y1, .......,yn be the value of y = f (x) corresponding to the arguments x0, x1, ..........,xn.Then from the definition of divided differences,we have
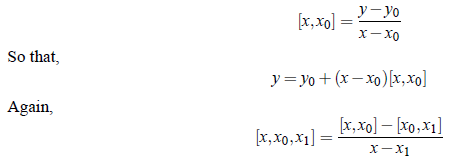
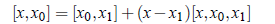
Substituting this value of [x, x0] in the above equation,we get
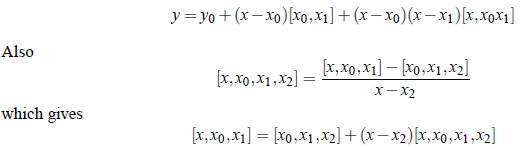
Substituting this value of [x, x0, x1] in the above equations, we obtain;
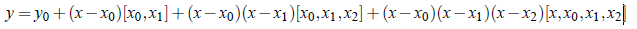
which is called Newton’s General Interpolation Formula with Divided Differences.