Regular Falsi Method
Regular Falsi Method:
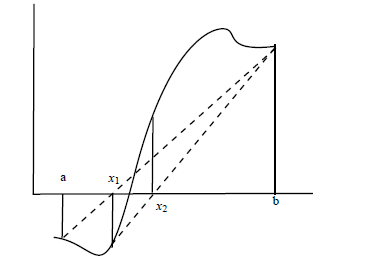
This method is also called as false position method. Consider the equation Bisection Method. Let a and b, such that a < b, be two values of x such that f (a) and f (b) are of opposite signs. Then the graph of y = f (x) crosses the x-axis at some point between a and b.
The equation of the chord joining the two point (a, f (a)) and (b, f (b)) is,
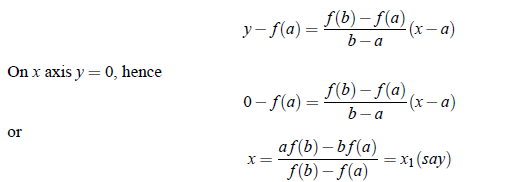
Now if function is considered as a straight line, the intersection of chord produces as approximate root value. Further very similar to Bisection Method root lies in between a and x1 or between x1 and b, depends upon the fact f (a) f (x1) < 0 or f (x1) f (b) < 0 respectively. Thus we may concentrate on smaller interval in which root lies. We repeat this process with interval in which root lies. Suppose that we are given an interval [a,b] satisfying Bisection Method and an error tolerance ε > 0. Then the Regula Falsi Method is consists of the following steps:
Figure of Regular Falsi Method:
R1. Compute c 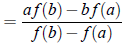
R2. If the difference with two consecutive c is less than or equal to ε, then accept c as the root and stop the procedure.
R3. If f (a). f (c) ≤ 0, then set b = c else, set a = c. Go to step B1.