Side Frequencies And Side Bands

Side Frequencies and Side Bands

The modulation theorem as described above, assumed transient data signals with associated continuous Fourier spectra.

 The same ideas are applicable as well to periodic signals (with discrete spectra).

 This case can be analyzed by directly using the Fourier integral transform. In that case, however, we will have to cope with impulsive spectral lines.

Alternatively, Fourier series expansion may be employed thereby avoiding the introduction of impulsive discrete spectra into the analysis.

 however, no analysis is actually needed for the case of periodic signals because the final answer can be deduced from the results for a transient signal.

 Specifically, in the Fourier series expansion of the data signal, each frequency component fo with amplitude a/2 will be shifted by ±fo to the two new frequency locations fc fo and -fc fo with anassociated amplitude aac/4. The negative frequency component -fo should also be considered in the same way.

 Note that the modulated signal does not have a spectral component at the carrierfrequency fc but rather, on each side of it, at fc±fo. Hence, these spectral components are termed sidefrequencies. When a band of side frequencies is present, it is termed a side band. Side frequencies are veryuseful in fault detection and diagnosis of rotating machinery.

Application of Amplitude Modulation

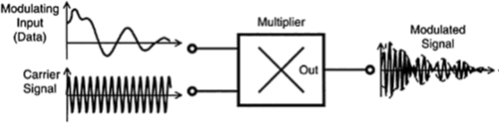
The main hardware component of an amplitude modulator is an analog multiplier. It is commercially available in the monolithic IC form. Alternatively, one can be assembled using integrated-circuit op-amps and various discrete circuit elements.

 Schematic representation of an amplitude modulator. In practice, in order to achieve satisfactory modulation, other components such as signal preamplifiers and filters would be needed.

There are many applications of amplitude modulation. In some applications, modulation is performed intentionally. In others, modulation occurs naturally as a consequence of the physical process, and the resulting

signal is used to meet a practical objective.

Typical applications of amplitude modulation include the following:

1.       Conditioning of general signals (including dc, transient, and low-frequency) by exploiting the advantages ofac signal conditioning hardware.

Representation of an amplitude modulator.

2.       Improvement of the immunity of low-frequency signals to low-frequency noise.

3.       Transmission of general signals (dc, low-frequency etc.) by exploiting the advantages of ac signals.

4.       Transmission of low-level signals under noisy conditions.

5.       Transmission of several signals simultaneously through the same medium (e.g., same telephone line, same transmission antenna, etc.)

6.       Fault detection and diagnosis of rotating machinery.