State Models

State Models

A state vector x is a column vector, which contains a minimum set of state variables (x1, x2… xn) which completely determine the state of the dynamic system. The number of states variables (n), is the order of the system.

Property 1

The state vector x(t0) at time t0 and the input (forcing excitation) u[t0, t1] over the time interval [t0, t1], will uniquely determine the state vector x(t1) any future time t1. In other words, a transformation g can be defined such that

x(t1)=g(t0, t1, x(t0), u[t0, t1])

Note that by the causality property of a dynamic system, future states can be determined if all inputs up to that future time are known. This means that the transformation g is no anticipative (i.e., inputs beyond t1 are not needed to determine x(t1). Each forcing function u [t0, t1] defines a state trajectory. As mentioned before, the dimensional vector space formed by all possible state trajectories is the state space.

Property 2

The state x(t1) and the input u(t1) at any time t1 will uniquely determine the system output or response vector y (t1) at that time. This can be expressed as

y(t1)=h(t1, x(t1), u(t1))

This says that the system response (output) at time t1 depends on the time, the input, and the state vector. The transformation h has no memory—the response at a previous time cannot be determined through the knowledge of the present state and input. Note also that, in general, system outputs (y) are not identical to the states (x) even though the former can be uniquely determined by the latter.

A state model consists of a set of n first-order ordinary differential equations (time-domain) that are coupled (inter-related). In vector form, this is expressed as

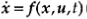
y=h(x, u, t)