A Multilayer Perceptron

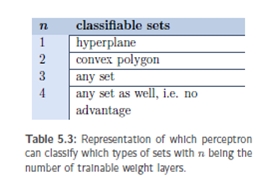
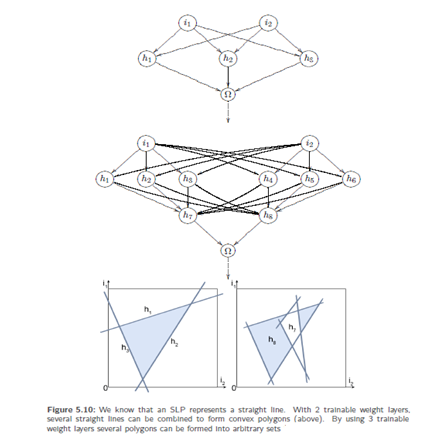
Introduction: -A perceptron with two or more trainable weight layers is called multilayer perceptron or MLP.It is more powerful than an SLP. A single layer perceptron can divide the input space by means of a hyper plane (in a two-dimensional input space by means of a straight line). A two stage perceptron can classify convex polygons by further processing these straight lines, e.g. in the form "recognize patterns lying above straight line 1, below straight line 2 and below straight line3. A multilayer perceptron represents an universal function approximator.

Perceptrons with more than one layer of variably weighted connections are referred to as multilayer perceptrons (MLP).An n-layer or n-stage perceptron has thereby exactly n variable weight layers and n 1 neuron layers () with neuron layer 1 being the input layer.

Since three-stage perceptron’s can classify sets of any form by combining and separating arbitrarily many convex polygons, another step will not be advantageous with respect to function representations. Be cautious when reading the literature: There are many different definitions of what is counted as a layer. Some sources count the neuron layers, some count the weight layers. Some sources include the retina, some the trainable weight layers. Some exclude the output neuron layer. Ann-stage perceptron has exactly n trainable weight layers. We now want to face the challenge of training perceptrons with more than one weight layer.