A Single Layer Perceptron
Introduction:-A single layer perceptron (SLP) is a perceptron having only one layer of variable weights and one layer of output neurons Ω.
Certainly, the existence of several output neurons Ω 1, Ω2. . . Ω n does not considerably change the concept of the perceptron .A perceptron with several output neurons can also be regarded as several different perceptron with the same input
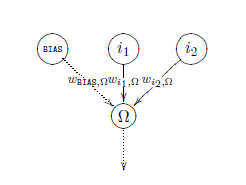
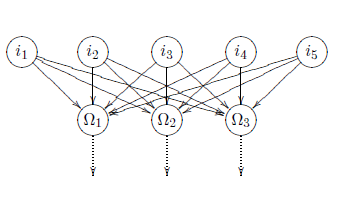
Single layer perceptron with two input neurons and one output neuron Single layer perceptron with several output neurons
Perceptron learning algorithm
The original perceptron learning algorithm with binary neuron activation function is described in alg. It has been proven that the algorithm converges in finite time so in finite time the perceptron can learn anything.
Suppose that we have a single layer perceptron with randomly set weights which we want to teach a function by means of training samples. The set of these training samples is called P. It contains, as already defined, the pairs (p, t) of the training samples p and the associated teaching input t.
Ø x is the input vector and 
Ø y is the output vector of a neural network,
Ø output neurons are referred to as
Ø i is the input and
Ø O is the output of a neuron.
Ø The error vector Ep represents the difference (t−y) under a certain training sample p.
Ø Furthermore, let O be the set of output neurons and
Ø I be the set of input neurons.
The error function
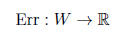
Regards the setof weights W as a vector and maps the values onto the normalized output error. It is obvious that a specific error function can analogously be generated for a single pattern p.