Components And Structure Of An Rbf Network
Introduction:-In an RBF network the output neurons only contain the identity as activation function and one weighted sum as propagation function. Thus, they do little more than adding all input values and returning the sum.Hidden neurons are also called RBF neurons (as well as the layer in which they are located is referred to as RBF layer). As propagation function, each hidden neuron calculates a norm that represents the distance between the input to the network and the so-called position of the neuron. This is inserted into a radial activation function which calculates and outputs the activation of the neuron.
The center Ch of an RBF neuron h is the point in the input space where the RBF neuron is located .In general the closer the input vector is to the center vector of an RBF neuron, the higher is its activation.
RBF neurons h have a propagation function fprop that determines the distance between the center Ch of a neuron and the input vector y. This distance represents the network input. Then the network input is sent through a radial basis function fact which returns the activation or the output of the neuron. RBF neurons are represented by the symbol 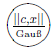
RBF output neurons use the weighted sum as propagation function fprop, and the identity as activation function fact. They are represented by the symbol 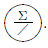
RBF network has exactly three layers in the following order: The input layer consisting of input neurons, the hidden layer (also called RBF layer) consisting of RBF neurons and the output layer consisting of RBF output neurons. Each layer is completely linked with the following one, shortcuts do not exist it is a feed forward topology. The connections between input layer and RBF layer are unweighted, i.e. they only transmit the input. The connections between RBF layer and output layer are weighted. The original definition of an RBF network only referred to an output neuron, but – in analogy to the perceptrons – it is apparent that such a definition can be generalized. A bias neuron is not used in RBF networks. The set of input neurons shall be represented by I, the set of hidden neurons by H and the set of output neurons by O.
Therefore, the inner neurons are called radial basis neurons because from their definition follows directly that all input vectors with the same distance from the center of a neuron also produce the same output value.