Crisp And Non-crisp Set

Description:-

− If characteristic function µ_A(x)  has only values 0 ('false')  and 1 ('true'').   Such  sets  are  crisp sets. 

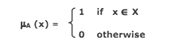
 − For Non-crisp sets the characteristic  function   µA(x)  can be defined. 

· The characteristic function   µ_A(x) for the crisp set is generalized for the Non-crisp sets.

· This generalized characteristic function  µ_A(x) is called membership function. 

Such Non-crisp sets are  called  Fuzzy Sets.

− Crisp set theory is not capable of representing descriptions and classifications in many cases; In fact, Crisp set does not provide adequate representation for most cases. 

 − The proposition of  Fuzzy Sets  are  motivated by the need to capture and represent real world data with  uncertainty due to imprecise measurement. 

−  The  uncertainties  are  also  caused  by  vagueness  in  the  language.

Representation of  Crisp  and  Non-Crisp Set

Example :  Classify students for a basketball team .This example explains the grade of truth value.

-  tall students qualify and  not tall students do not qualify

-  if students 1.8 m tall are  to be qualified, then   should  we exclude  a student who  is 1/10" less?  or  should  we exclude  a student who is 1" shorter?

Non-Crisp Representation to represent the notion of a tall person.

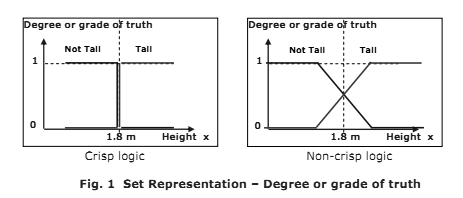
A student of height 1.79m would belong to both tall and not tall sets  with a particular degree of membership.   As the height increases the membership grade within the tall set would  increase whilst the membership grade within the not-tall set would decrease.  

Examples of Crisp Set

Example 1:  Set of prime numbers  ( a crisp set)

if we consider space X   consisting of  natural numbers   ≤   12 

           i.e  X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Then, the set of prime numbers could be described as follows. 

PRIME = {x contained in X | x is a prime number} = {2, 3, 5, 6, 7, 11}