Linear Separability
Introduction:-Linear separability is a powerful technique which is used to learn complicated concepts that are considerably more complicated than just hyperplane separation.
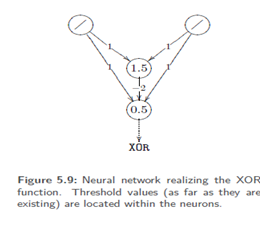
Let f be the XOR function which expects two binary inputs and generates a binary output .Let us try to represent the XOR function by means of an SLP with two input neurons i1, i2 and one output neuron
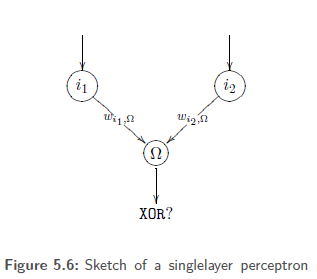
Here we use the weighted sum as propagation function, a binary activation function with the threshold value and the identity as output function. Depending on i1 and i2has to output the value 1 if the following holds:
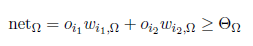-----(1)
We assume a positive weight wi2,Ω the inequality is then equivalent to
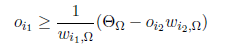-------(2)
With a constant threshold value ƟΩ, the right part of in equation 2 is a straight line through a coordinate system defined by the possible outputs oi1 und oi2 of theinput neurons i1 and i2
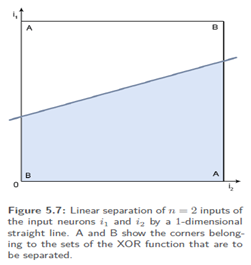For a positive wi2,Ω the output neuron fires forinput combinations lying above the generated straight line. For a negative wi2,Ω it would fire for all input combinations lying below the straight line. Note that only the four corners of the unit square are possible inputs because the XOR function only knows binary inputs.
In order to solve the XOR problem, we have to turn and move the straight line so that input set A = {(0, 0), (1, 1)} is separated from input set B = {(0, 1), (1, 0)} this is, obviously, impossible. Generally, the input parameters of n man inputneurons can be represented in an n dimensional cube which is separated by an SLP through an (n−1)-dimensional hyper plane. Only sets that can be separatedby such a hyper plane, i.e. which are linearly separable, can be classified by an SLP.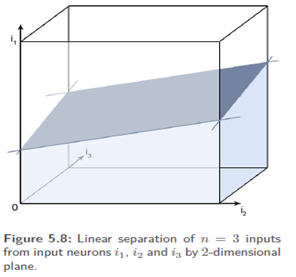
Unfortunately, it seems that the percentage of the linearly separable problems rapidly decreases with increasing, which limits the functionality ofthe SLP. Additionally, tests for linear separability are difficult. Thus, for more difficult tasks with more inputs we need something more powerful than SLP. The XOR problem itself is one of these tasks, since a perceptron that is supposed to represent the XOR function already needs a hidden layer.
