Resilient Backpropagation

Introduction: -Resilient backpropagation is an extension to backpropagation of error.On the one hand, users of backpropagation can choose a bad learning rate. On the other hand, the further the weights are from the output layer, the slower backpropagation learns. For this reason, MartinRiedmiller et al. enhanced backpropagation and called their version resilient backpropagation.

Learning rates: Backpropagation uses by default a learning rate which is selectedby the user, and applies to the entire network.It remains static untilit is manually changed. Rprop pursues acompletely different approach: there is no global learning rate. First, each weight w_i,jhas its own learning rateɳi,j, and second, these learning rates are not chosen by the user, but are automatically set by R_prop itself. Third, the weight changes are not static butare adapted for each time step of R_prop.

Weight change: When using backpropagation, weights are changed proportionally to the gradient of the error function. At first glance, this is really intuitive. However, we incorporate every jagged feature of the error surface into the weight changes. It is at least questionable, whether this is always useful. Here, Rprop takes other way as well: the amount of weight change Δw_i,jsimply directly corresponds to the automatically adjusted learning rate ɳ_i,j. Thus the change in weight isnot proportional to the gradient,it isonly influenced by the sign of the gradient. Until now we still do not know how exactly the ɳ_i,j are adapted atrun time, but let me anticipate that the resulting process looks considerably less rugged than an error function.

Weight changes are notproportional to the gradient:-Let us first consider the change in weight.The weightspecificlearning rates directly serve as absolutevalues for the changes of the respectiveweights. There remains the questionof where the sign comes from this is a point at which the gradient comesinto play. As with the derivation of backpropagation,we derive the error function Err(W) by the individual weights w_i,j and obtain gradients .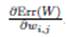

Now, the big difference: rather than multiplicatively incorporating the absolute value of the gradient into the weight change, we consideronly the sign of the gradient. The gradient hence no longer determines the strength, but only the direction of the weight change. If the sign of the gradient is positive, we must decrease the weight wi,j.So the weight is reduced by ɳ_i,j. If thesign of the gradient is negative, the weightneeds to be increased. If the gradient isexactly 0, nothing happens at all. Let us now create a formulafrom this colloquial description. The corresponding terms are affixed with a (t)to show that everything happens at thesame time step. we shorten the gradient

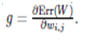
Weight change in R_prop