Training Patterns And Teaching Input
Introduction:-In case of supervised learning we assume a training set consisting of training patterns and the corresponding correct output values we want to at the output neurons after the training. While the network has not finished training,i.e. as long as it is generating wrong outputs, these output values are referred to as teaching input and that for each neuron individually. Thus, for a neuron j with the incorrect output oj ,tj is the teaching input, which means it is the correct or desired output for a training pattern p.
A training pattern is an input vector p with the components p1, p2. . . pn whose desired output is known. By entering the training pattern into the network we receive an output that can be compared with the teaching input, which is the desired output. The set of training patterns is called P. It contains a finite number of ordered pairs (p, t) of training patterns with corresponding desired output.Training patterns are often simply called patterns, that is why they are referred to as p.
The teaching input tj is the desired and correct value j should output after the input of a certain training pattern. Analogously to the vector p the teaching inputs t1, t2, . . . , tn of the neurons can also be combined into a vector t. t always refers to a specific training pattern p and is, as already mentioned, contained in the set P of the training patterns.
Error vector:-For several output neurons, the difference between output vector and teaching input under a training input p
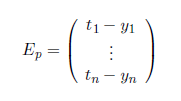
Is referred to as error vector, sometimes it is also called difference vector. Depending on whether you are learning offline or online, the difference vector refers to a specific training pattern, or to the error of a set of training patterns which is normalized in a certain way.
Summary:-There is the input vector x, which can be entered into the neural network. Depending on the type of network being used the neural network will output an output vector y. Basically, the training sample p is nothing more than an input vector. We only use it for training purposes because we know the corresponding teaching input t which is nothing more than the desired output vector to the training sample. The error vector Ep is the difference between the teaching input t and the actual output y.
So, what x and y are for the general network operation are p and t for the network training and during training we try to bring y as close to t as possible. One advice concerning notation: We referred to the output values of a neuron i as oi. Thus, the output of an output neuron Ωis called oΩ. But the output values of a network are referred to as yΩ. certainly, these network outputs are only neuron outputs, too, but they are outputs of output neurons. In this respect
yΩ= oΩ
is true.