Weight Matrix
Introduction:-The aim is to generate minima on the energy surface, so that at an input the network can converge to them. As with many other network paradigms, a set P of training patterns p ϵ {1,−1}|K|, representing the minima of our energy surface. Here we do not look for the minima of an unknown error function but define minima on such a function. The purpose is that the network shall automatically take the closest minimum when the input is presented. The training of a Hopfield network is done by training each training pattern exactly once.
Single Shot Learning where pi and pj are the states of the neurons i and j under p ϵ P:
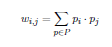
This results in the weight matrix W. We initialize the network by means of a training pattern and then process weights wi,j one after another.
For each of these weights we verify: Are the neurons i, j n the same state or do the states vary? In the first case we add 1to the weight, in the second case we add −1.This we repeat for each training pattern p 2 P. Finally, the values of the weights wi,j are high when i and j corresponded with many training patterns.This high value tells the neurons: “Often, it is energetically favorable to holdthe same state". The same applies to negative weights. Due to this training we can store a certainfixed number of patterns p in the weightmatrix. At an input x the network willconverge to the stored pattern that is closestto the input P unfortunately, the number of the maximumstorable and reconstructiblepatternsp is limited to
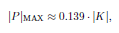
Which in turn only applies to orthogonal patterns.
Learning rule for Hopfield networks. The individual elements of the weight matrix W are defined by a single processing of the learning rule
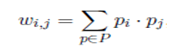
Where the diagonal of the matrix is covered with zeros. Here, no more than |K| training samples can be trainedand at the same time maintain their function. Now we know the functionality of Hopfield networks but nothing about their practical use.